复习向，Crafting Interpreters 中介绍的两种方法

表达式定义

简单起见，算数表达式只包含以下元素：

• 整数
• 括号
• 一元运算符：-
• 二元运算符：+ - * /

比如-1 + 2*(1 + 3 - 2)

Lexer

第一步将输入表达式分成小单位的token，因为表达式内容较少，只用产出如下组件：

• 整数
• (
• )
• +
• -
• *
• /

表达式-112 + 2*(1 + 3 - 42) 产出的token序列为-, 112, +, 2, *, (, 1, +, 3, -, 42, ), None

此外增加peek功能，方便后续解析，Lexer如下

class Lexer:
    def __init__(self, expr: str):
        self.expr_str = expr
        self.peeked = None
        self.tokens = self.tokens_iter()

    def tokens_iter(self):
        num = None
        for ch in self.expr_str:
            if ch.isdigit():
                if num:
                    num = 10 * num + int(ch)
                else:
                    num = int(ch)
            else:
                if num is not None:                    
                    yield num # yield an int
                    num = None
                if ch != ' ':                    
                    yield ch # yield an operation
        if num:
            yield num

    def next(self):
        """consume next token and return it
        None means end of the token stream
        """
        if self.peeked is not None:
            ret = self.peeked
            self.peeked = None
        else:
            try:
                ret = next(self.tokens)
            except StopIteration:
                return None
        return ret

    def peek(self):
        """peek the next token without consuming it 
        """
        if self.peeked is None:
            self.peeked = self.next()
        return self.peeked

EvalBase

写一个求值的基类，把Lexer组合进去，复用一点代码

class Eval:
    def __init__(self, expr: str):
        self.lexer = Lexer(expr)

    def next(self):
        return self.lexer.next()

    def peek(self):
        return self.lexer.peek()

递归下降

• 编程领域的语言都有明确的生成规则，算术表达式的生成规则如下：

  1. expr: factor ( ('+' | '-') factor )*
  2. factor: unary ( ('*' | '/') unary)*
  3. unary: '-'? unary | primary
  4. primary: num | '(' expr ')'

• 从上往下，计算的优先级依次升高，问题的求解规模减少，直到遇到计算数据的基本单位，一个整形num。

• 所谓递归下降，就把每个生成规则都做成一个函数，调用更规模更小的子问题，子问题的优先级一般会更高，如果同级，就表示右结合的运算，比如一元运算符-。
• 易错点是写出无限循环，自己调用自己，问题规模没有减小，就是常说的直接、间接左递归
• 每一个函数完整控制着表达式中的一个计算单元，可以利用他们的返回值进行运算。

class Descent(Eval):
    def primary(self):
        token = self.next()
        if isinstance(token, int):
            return token
        elif token == '(':
            ret = self.expr()
            assert ')' == self.next(), 'unbalanced parentheses'
            return ret
        else:
            raise ValueError(f'unrecognized token {token!r}')

    def unary(self):
        token = self.peek()
        if token == '-':
            self.next()
            return - self.unary()
        else:
            return self.primary()

    def factor(self):
        left = self.unary()
        while self.peek() in ('*', '/'):
            op = self.next()
            if op == '*':
                left *= self.unary()
            elif op == '/':
                left //= self.unary()
            else:
                raise ValueError(f'unrecognized operator {op!r}')
        return left

    def expr(self):
        left = self.factor()
        while self.peek() in ('+', '-'):
            op = self.next()
            if op == '+':
                left += self.factor()
            elif op == '-':
                left -= self.factor()
            else:
                raise ValueError(f'unrecognized operator {op!r}')
        return left

    def eval(self):
        return self.expr()

Pratt方法

• 每一次表达式解析，都是将一个表达式看作 一个前缀表达式 (若干中缀表达式)*进行收集，求值后入栈，该次收集的表达式所涉及的操作数的优先级，一定不高于参数所给定的优先级。比如1 + 2 + 3解析，参数为最低优先级：前缀表达式1，中缀表达式+ 2，中缀表达式+ 3。两个中缀表达式去掉操作符后，再递归调用表达式解析，各自通过两个前缀表达式得到 2 和 3。

• 收集函数根据token进行查找确定。同样的-，可以分发到作为前缀的unary，也可以分发到作为中缀的bianry，视上下文而定。

• 中缀表达式的停止，用操作符的优先级来进行，比如1 + 2 + 3中，+ 操作符分发的binary开启的新一轮表达式收集，只能包含比自己更高的操作符，比如* /，看到2后面的+号和自己同级，于是停止，形成一个左结合的操作。

• 需要一个最低的优先级Null，可以停止一切中缀表达式的匹配。
• 和递归下降的模拟生成规则的函数不同，Pratt中的分发函数属于收集函数，只会根据优先级收集计算单元的某部分，没有完整信息，所以需要使用栈记录信息并求值。

代码方面，首先记录运算符的优先级，而递归下降中的类似

from enum import Enum
class Prec(Enum): # precedence
    Null = auto()
    Term = auto()     # '+ -' 
    Factor = auto()   # '* /'
    Unary = auto()    # '-'
    Primary = auto()  # num '(' expr ')'

    def next(self):
        """return the next level precedence
        Prec.Primary will return itself"""
        return Prec(min(self.value + 1, self.Primary.value))

    def __le__(self, other: 'Prec'):
        return self.value <= other.value

新建一个Pratt类，主要构建出根据token进行分发的函数表格。

• 加入Prec信息和prec_of，是因为合并了一些逻辑，比如binary的参数token可能横跨两个优先级，需要识别出以继续收集。事实上，如果没有合并，每个收集函数，对自己该继续收集什么层级的表达式，都是清楚的，比如之后会看到的unary直接调用parse_with(Prec::Unary)，这也是-在表中只记录它在binary中的优先级的原因。
• 默认返回的优先级是Null，所以最后的中止token为None，可以用来跳出所有中缀表达式的调用，结束解析
• stack用来求值

@dataclass
class DispatchEntry:
    prefix: MethodWrapperType = None
    infix: MethodWrapperType = None
    prec: Prec = Prec.Null


EmptyEntry = DispatchEntry()


class Pratt(Eval):

    def __init__(self, expr: str):
        super().__init__(expr)
        self.stack = []
        self.index_map = {
            'num': DispatchEntry(self.num, None, Prec.Null),
            '+': DispatchEntry(None, self.binary, Prec.Term),
            '-': DispatchEntry(self.unary, self.binary, Prec.Term),
            '*': DispatchEntry(None, self.binary, Prec.Factor),
            '/': DispatchEntry(None, self.binary, Prec.Factor),
            '(': DispatchEntry(self.group, None, Prec.Null)
        }

    def fetch_entry(self, token: str):
        if token and isinstance(token, int):
            token = 'num'
        return self.index_map.get(token, EmptyEntry)

    def prefix_fn_call(self, token: str):
        if fn := self.fetch_entry(token).prefix:
            return fn(token)
        raise ValueError(f'unkown token to dispatch prefix: {token!r}')

    def infix_fn_call(self, token: str):
        if fn := self.fetch_entry(token).infix:
            return fn(token)
        raise ValueError(f'unkown token to dispatch infix: {token!r}')

    def prec_of(self, token: str):
        return self.fetch_entry(token).prec

然后加入被分配的收集函数

# in class Pratt
    def parse_with(self, prec: Prec):
        token = self.next()
        self.prefix_fn_call(token)
        while prec <= self.prec_of(self.peek()):
            token = self.next()
            self.infix_fn_call(token)

    def unary(self, token: str):
        self.parse_with(Prec.Unary)
        if token == '-':
            self.stack[-1] = -self.stack[-1]

    def binary(self, token):
        self.parse_with(self.prec_of(token).next())
        right = self.stack.pop()
        left = self.stack.pop()
        if token == '+':
            self.stack.append(left + right)
        elif token == '-':
            self.stack.append(left - right)
        elif token == '*':
            self.stack.append(left * right)
        elif token == '/':
            self.stack.append(left // right)

    def group(self, token):
        self.expr()
        assert ')' == self.next(), 'unbalanced parentheses'

    def num(self, token: int):
        self.stack.append(token)

    def expr(self):
        self.parse_with(Prec.Null.next())

    def eval(self):
        self.expr()
        return self.stack[-1]

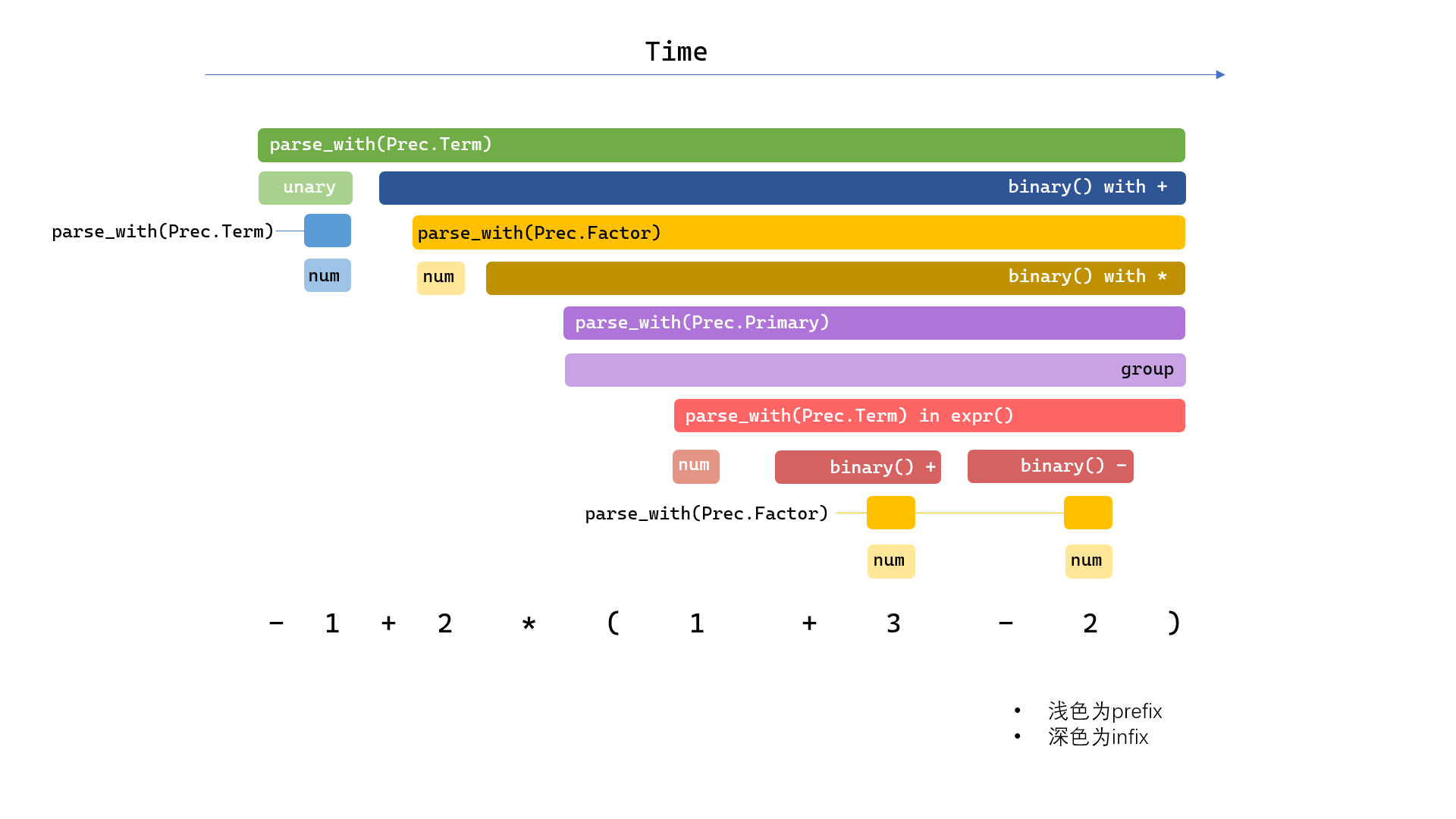
画了一个调用栈来表示解析过程，paser_with都用主色表示，它所引发的prefix调用都用浅色表示，所引发的infix调用使用深色。

结论

• 递归下降中的规则从上往下，优先级上升，问题规模下降
• Pratt方法的核心是parse_with(prec :Prec) { 前缀表达式 (中缀表达式)*}将下一个表示式的值入栈，该值的求解过程中使用的操作数，都大于等于prec优先级
• Pratt中的prec_of出现是因为收集函数的逻辑合并
• Pratt方法中的最小逻辑用来跳出中缀匹配